En la entrada anterior introducimos el algoritmo k nearest neighbors o de los vecinos más cercanos. Os conté como funciona el algoritmo y os presenté un ejemplo que clasificaba puntitos en un espacio en dos dimensiones. Como sé que os quedasteis con ganas de más (sí, aún os oigo suplicar que os cuente más) vamos a poner a prueba al algoritmo k-nn para ver si es capaz de aprender a reconocer caracteres manuscritos (problema conocido como OCR o reconocimiento óptico de caracteres). Como en el anterior artículo, os dejo un enlace al notebook de Jupyter que he usado para escribir este post: https://github.com/albgarse/InteligenciaArtificial/blob/master/Machine%20Learning/KNN%20Image%20Classifier.ipynb
Para entrenar nuestro reconocedor de caracteres vamos a usar un dataset bastante conocido: MNIST. Desde esta web podéis descargar los cuatro archivos que lo componen:
train-images-idx3-ubyte.gz: imágenes de entrenamiento
train-labels-idx1-ubyte.gz: etiquetas de las imágenes de entrenamiento
t10k-images-idx3-ubyte.gz: conjunto de imágenes para test
t10k-labels-idx1-ubyte.gz: conjunto de etiquetas de las imágenes de test
Este dataset contiene miles de imágenes con dígitos escritos a mano. En la imagen de cabecera de este artículo puedes ver qué pinta tienen los dígitos. Las imágenes están codificadas dentro del archivo con un formato que está descrito en la web. No voy a entrar en detalles porque todo está ahí. Simplemente os pongo el código que he usado para cargarlas e introducirlas en matrices de NumPy.
def loadMNIST( prefix, folder ):
intType = np.dtype( 'int32' ).newbyteorder( '>' )
nMetaDataBytes = 4 * intType.itemsize
data = np.fromfile( folder + "/" + prefix + '-images.idx3-ubyte', dtype = 'ubyte' )
magicBytes, nImages, width, height = np.frombuffer( data[:nMetaDataBytes].tobytes(), intType )
data = data[nMetaDataBytes:].astype( dtype = 'float32' ).reshape( [ nImages, width, height ] )
labels = np.fromfile( folder + "/" + prefix + '-labels.idx1-ubyte',
dtype = 'ubyte' )[2 * intType.itemsize:]
return data, labels
images_tr, labels_tr = loadMNIST( "train", "./mnist" )
images_te, labels_te = loadMNIST( "t10k", "./mnist" )
# imagenes en array de 60000 x 28 x 28 -> 60000 imagenes de 28x28
El conjunto de entrenamiento tiene 60.000 imágenes y el de test, es decir, el que usaremos para poner a prueba el sistema una vez entrenado, dispone de 10.000 imágenes. Cada una de estas imágenes es una matriz de 28x28 píxeles con un dígito del 0 al 9 dibujado a mano. Si recordáis, en el ejemplo del artículo anterior manejábamos datos de dos dimensiones (por ejemplo, el sueldo y la deuda a la hora de conceder o no un préstamo). Ahora trabajamos con datos de 784 dimensiones (28*28 píxeles). Así que por lo visto vamos a tener que sumar, restar, elevar al cuadrado y hacer raíces cuadradas de matrices de 784 elementos. No está mal ¿verdad? veremos como le sienta esto a NumPy.# coger un dígito aleatorio del grupo de test i = random.randint(0,images_te.shape[0]) img_test = images_te[i].flatten() label_test = labels_te[i]Empezamos por elegir una imagen aleatoria del conjunto de test para ver si somos capaces de clasificarla correctamente y reconocer el dígito. Para operar con la imagen la aplanamos (flatten), es decir, ponemos toda la matriz en una sola fila (matriz de 1x784). También guardamos su etiqueta para compararla con la clasificación que haga el algoritmo.
# buscamos los vecinos más cercanos (KNN)
k = 5 #número de vecinos
distances = []
for i in range(images_tr.shape[0]):
dist = np.sqrt(np.sum(np.square(images_tr[i].flatten() - img_test)))
distances.append((dist, labels_tr[i])) # guardamos las etiquetas y la distancia
#ordenamos por distancia y nos quedamos con los k vecinos más cercanos
distances.sort(key=lambda x: x[0])
neighbors = distances[:k]
Ahora buscamos a los k vecinos más cercanos (en este caso k=5). Si recuerdas el ejemplo anterior, el código era algo más complejo debido a que estábamos clasificando varios datos de test. En este caso sólo clasificamos un dato (el dígito que hemos seleccionado aleatoriamente en el código de más arriba). No entro en mucho detalle ya que en el artículo anterior ya os conté cómo funcionaba. Si no entiendes qué hace este fragmento de código dale un repaso a lo que ya os conté sobre k-nn.# contamos los votos para ver qué etiqueta gana
votes = [0,0,0,0,0,0,0,0,0,0]
for neighbor in neighbors:
votes[neighbor[1]] = votes[neighbor[1]] + 1
# obtenemos la etiqueta ganadora
pred_label = votes.index(max(votes))
Una vez elegidos los k vecinos más cercanos toca votar (k-nn es una democracia). Por lo tanto, recontamos las etiquetas de los k vecinos más cercanos y la ganadora será nuestra predicción.print ("Predicted: " + str(pred_label))
print ("Real: " + str(label_test))
img = plt.imshow(img_test.reshape(28,28), cmap="gray")
display(img)
La siguiente imagen muestra una captura de la ejecución del código.Y ¡parece que funciona!
Pero ¿qué tasa real de acierto consigue k-nn con el dataset MNIST? Si tenéis curiosidad os propongo que probéis con todo el conjunto de test. Eso sí, son 10.000 imágenes de prueba, así que un poco de paciencia cuando lancéis la ejecución. En la prueba que yo he hecho contra todo el conjunto de test, de las diez mil imágenes el algoritmo ha clasificado correctamente 9.688. Esto es, una tasa de acierto de 0.968 (9.688 / 10.000). O lo que es lo mismo, ha acertado un 96,8% de las veces. No está nada mal ¿verdad?
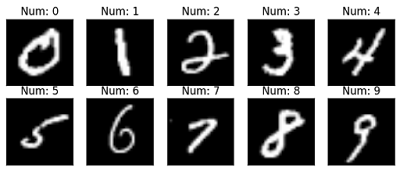

Comentarios
Publicar un comentario